
This is not as difficult as it may seem. After doing it a few times on a scientific calculator you probably won't even need the recipe.
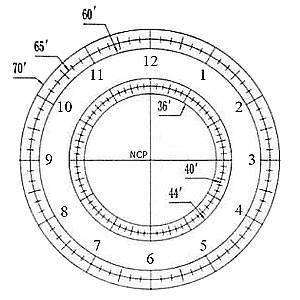
At right is the illuminated scale seen in the iOptron's polar alignment scope. Because Polaris is offset from the true North Celestial Pole (NCP) by about 2/3rds of degree, the goal is to place the Polaris at the proper clock position on the inner set of circles for the time at which the alignment is being done. The crosshairs at center will then coincide with the position of the NCP. This is accomplished by adjusting the azimuth and tilt (elevation/altitude) of the Sky Tracker, the latter by suitably turning the geared latitude adjustment knob before locking it in place. (The outer set of circles is for setting on the South Celestial Pole using σ Octantis in the Southern Hemisphere, which is a little more than a degree away from the pole there.)
The Local Sidereal Time (LST) is just the Right Ascension (RA) of whatever astronomical object is on the meridian at that moment. If you're setting up and getting polar aligned ½ hour or an hour before the object you wish to observe transits (the meridian), subtract that much time from the object's RA to get the LST to use.
If you desire, a small, free, digital desktop LST clock, with the name RSclock (.exe), is available from Radio-Sky Publishing, at least for Windows operating systems (probably also for other popular ones). A search for sidereal clock programs should turn up a copy fairly easily. I've used it on several machines, it's easy to install, and works without a hitch. I have it set up so it starts every time the system boots up, because I like having a clock with seconds (unlike the standard Windows clock in the system "tray"). You'll need to have your longitude handy so it can calculate your local ST.
With those preliminaries, here's what to do:

Local Sidereal Time (LST) → iOptron Sky Tracker Polaris setting
Example/check: For LST = 18:04, 10:24 is the result. (On 9/1/2017 this is 7:30 PM MST)
The result of steps #2 and #3 is the hour angle (HA) of Polaris, the fundamental equation of observational astronomy being HA = RA - LST. When this is positive and less than 12 hours, Polaris is east of the meridian; when it's negative it's west of the meridian up until -12 hours . At ±12 hours Polaris is directly below the (true) pole.
An LST of 14:52 (Polaris+12hrs), combined with the above RA for Polaris, converts to an iOptron "time" of 0/12 hours -- i.e., straight up, Polaris at the top of the scale.
The minus sign in front of the LST (via it being subtracted off) means the time on the iOptron scale counts down as time progresses, at the rate of 1 minute every two minutes of actual time (that dividing-by-two part above). The other way of looking at it is Polaris "goes against the clock" (or backwards) on the scale as time progresses; the image inversion doesn't change the counter-clockwise sense of rotation of Polaris around the scale. This is all reversed in the Southern Hemisphere.
An obvious alternative to steps #'s 5 and 6 would be to *subtract* six hours rather than add it if the result was going to be >12 hours.
As each day goes by, the LST will be 4 minutes more at the same local time, so the iOptron setting will be down 2 minutes from the day before. In the example above, two days later at 7:30 local time the LST will be 18:12 and the iOptron setting 10:20. So in that sense also Polaris goes against the clock over time, not just at the smaller timescale. I'm not sure right off if this is the same in the Southern Hemisphere or the other way around.

As for the distance of Polaris from the NCP, this changes very slightly over time, because of the precession of the equinoxes. This causes the celestial coordinates of everything -- Polaris included -- to change with time. Especially Polaris, because it is so close to the NCP. Its RA changes especially fast, as seen in the first table, while it's distance from the NCP changes more slowly, as seen in the second:
| RA of Polaris | Date | Julian Day Number | ||
| 2hr 50min | 7-30½-2014 | 2,456,869 | ||
| 2hr 52min | 11-05-2015 | 2,457,331½ | ||
| 2hr 54min | 3-31-2017 | 2,457,844 | ||
| 2hr 56min | 9-24½-2018 | 2,458,386 | ||
| 2hr 58min | 4-17-2020 | 2,458,956½ | ||
| 3hr 00min | 11-30-2021 | 2,459,548½ | ||
| 3hr 02min | 9-01-2023 | 2,460,188½ | ||
| 3hr 04min | 3-15-2025 | 2,460,749½ | ||
| 3hr 06min | 8-13-2026 | 2,461,265½ | ||
| 3hr 08min | 11-03-2027 | 2,461,712½ | ||
| 3hr 10min | 1-23-2029 | 2,462,159½ | ||
| NCP − Polaris | Date | JDN | ||
| 44' | 06-09½-2000 | 2,451,705 | ||
| 42' | 02-24½-2008 | 2,454,521 | ||
| 40' | 08-16½-2016 | 2,457,617 | ||
| 38' | 02-18½-2024 | 2,460,359 | ||
| 36' | 02-19-2034 | 2,464,012½ | ||
| 34' | 07-13½-2042 | 2,467,079 | ||
These numbers were determined using the free program Stellarium, v17. I'm not sure what constants they use for their precession calculations, but the program shows Polaris is closest to the NCP on 09-28½-2099 (JDN 2,487,975) at a distance of 27'25.1" .
©2017-22, Chris Wetherill. All rights reserved. Display of words or photos here does NOT constitute or imply permission to store, copy, republish, or redistribute my work in any manner for any purpose without expressed prior permission.


[ Back to Main VISNS Page ]