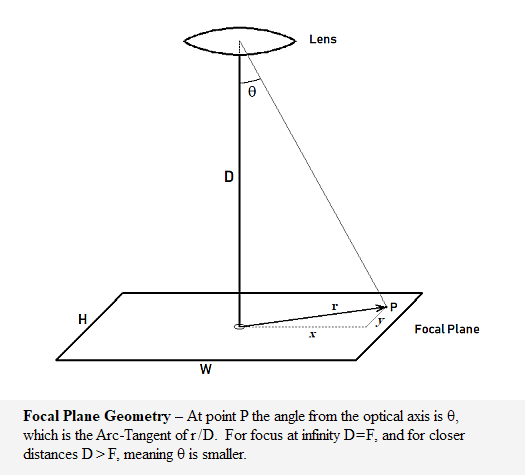
A well-known property of lenses is that their illumination level at the focal plane diminishes as one moves away from the optical axis. I won't go into the reasons why -- do a search on something called the Cosine-to-the-Fourth Law and you'll find plenty to read. Suffice it say geometry for a simple lens conspires in four ways, each time introducing a cosine factor, so the illumination level falls off away from the optical axis as Cos⁴Θ.

For a "normal" lens the focal length (F) is approximately equal to the sensor diagonal, which is twice the maximum radius, r_max. Therefore the maximum angle, to one of the corners, is Θ_max = Arc-Tangent( r_max / F) = Arc-Tangent(½) = 26.565°. Thus, Cos(Θ_max) = 0.894 and Cos⁴(Θ_max) = 0.64. This is a little less than 2/3rds of a stop. But this is a maximum. For most of the outer portions of the frame the factor is closer to ½ stop, and for lots of subject matter this is insignificant or so small it's never noticed.

With negative materials the effect is to some degree canceled out when an enlargement is made. The enlarging lens has a similar falloff as the taking lens did, so if the negative is a little bit thinner towards its edges and corners this is evened out by a comparable dimunition in the other direction by the enlarging lens. With slide material the two factors both operate in the same direction and the effect is doubled. With digital scanning there's no enlarging lens, so the effect now has to be taken into account with negatives (no longer being mostly compensated for) and factored in only once with slides.

The lens's field of view is 2 × Θ_max, or almost a radian for a "normal" focal length. With a view camera the ability to make adjustments, both side/side and up/down translations as well as lens tilt, requires a lens with a larger field of illumination than this, maybe something like 70° or 75° for this focal length. Lens specs often include a diameter of illumination, a linear rather than an angular measure. For 4x5, the film diagonal is about 150mm, or r_max = 75mm. But an inch of lateral movement is ~25mm's, so in practice an r_max of ~100mm is needed, which is a diameter of 200mm. This corresponds to Θ_max = Arc-Tangent( 2/3 )), which is above 67° for the angular diameter. This corresponds to a Cos⁴Θ factor at r_max of a little more than ½x, meaning 1.06 stops. With the camera back in portrait or vertical orientation it's possible to make use of this "feature" to darken clear blue skies progressively by putting the top of the frame near the edge of the field of illumination through the use of the camera's shift and tilt adjustments.